The Algebraic MultiGrid Preconditioners Package based on PSBLAS (AMG4PSBLAS) provides parallel Algebraic MultiGrid (AMG) preconditioners (see, e.g., [5, 31]), to be used in the iterative solution of linear systems,
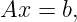 | (1) |
where A is a square, real or complex, sparse symmetric positive definite (s.p.d) matrix.
The preconditioners implemented in AMG4PSBLAS are obtained by combining 3 different types of AMG cycles with smoothers and coarsest-level solvers. Available multigrid cycles include the V-, W-, and a version of a Krylov-type cycle (K-cycle) [5, 27]; they can be combined with Jacobi, hybrid forward/backward Gauss-Seidel, block-Jacobi and additive Schwarz smoothers with various versions of local incomplete factorizations and approximate inverses on the blocks. The Jacobi, block-Jacobi and Gauss-Seidel smoothers are also available in the ℓ1 version [14].
An algebraic approach is used to generate a hierarchy of coarse-level matrices and operators, without explicitly using any information on the geometry of the original problem, e.g., the discretization of a PDE. To this end, two different coarsening strategies, based on aggregation, are available:
Either exact or approximate solvers can be used on the coarsest-level system. We provide interfaces to various parallel and sequential sparse LU factorizations from external packages, sequential native incomplete LU and approximate inverse factorizations, parallel weighted Jacobi, hybrid Gauss-Seidel, block-Jacobi solvers and calls to preconditioned Krylov methods; all smoothers can be also exploited as one-level preconditioners.
AMG4PSBLAS is written in Fortran 2003, following an object-oriented design through the exploitation of features such as abstract data type creation, type extension, functional overloading, and dynamic memory management. The parallel implementation is based on a Single Program Multiple Data (SPMD) paradigm. Single and double precision implementations of AMG4PSBLAS are available for both the real and the complex case, which can be used through a single interface.
AMG4PSBLAS has been designed to implement scalable and easy-to-use multilevel preconditioners in the context of the PSBLAS (Parallel Sparse BLAS) computational framework [22, 21]. PSBLAS provides basic linear algebra operators and data management facilities for distributed sparse matrices, kernels for sequential incomplete factorizations needed for the parallel block-Jacobi and additive Schwarz smoothers, and parallel Krylov solvers which can be used with the AMG4PSBLAS preconditioners. The choice of PSBLAS has been mainly motivated by the need of having a portable and efficient software infrastructure implementing “de facto” standard parallel sparse linear algebra kernels, to pursue goals such as performance, portability, modularity ed extensibility in the development of the preconditioner package. On the other hand, the implementation of AMG4PSBLAS, which was driven by the need to face the exascale challenge, has led to some important revisions and extentions of the PSBLAS infrastructure. The inter-process comunication required by AMG4PSBLAS is encapsulated in the PSBLAS routines; therefore, AMG4PSBLAS can be run on any parallel machine where PSBLAS implementations are available. In the most recent version of PSBLAS (release 3.7), a plug-in for GPU is included; it includes CUDA versions of main vector operations and of sparse matrix-vector multiplication, so that Krylov methods coupled with AMG4PSBLAS preconditioners relying on Jacobi and block-Jacobi smoothers with sparse approximate inverses on the blocks can be efficiently executed on cluster of GPUs.
AMG4PSBLAS has a layered and modular software architecture where three main layers can be identified. The lower layer consists of the PSBLAS kernels, the middle one implements the construction and application phases of the preconditioners, and the upper one provides a uniform interface to all the preconditioners. This architecture allows for different levels of use of the package: few black-box routines at the upper layer allow all users to easily build and apply any preconditioner available in AMG4PSBLAS; facilities are also available allowing expert users to extend the set of smoothers and solvers for building new versions of the preconditioners (see Section 6).
This guide is organized as follows. General information on the distribution of the source code is reported in Section 2, while details on the configuration and installation of the package are given in Section 3. The basics for building and applying the preconditioners with the Krylov solvers implemented in PSBLAS are reported in Section 4, where the Fortran codes of a few sample programs are also shown. A reference guide for the user interface routines is provided in Section 5. Information on the extension of the package through the addition of new smoothers and solvers is reported in Section 6. The error handling mechanism used by the package is briefly described in Section 7. The copyright terms concerning the distribution and modification of AMG4PSBLAS are reported in Appendix A.